From Mereology to the Basic Equation
The reasoning towards the basic equation starts from the "Top" axiom of mereology
There exists a "universal object", designated W, such that PxW (read “x is part of W”)
holds for any x, meaning that all x are part of W:
∃W ∀x [PxW] ("Top Axiom")
In the following a “quantification” of this logical expression is attempted.
The first step towards this quantification relates to the “all quantifier” ∀.
"All" initially is quantified as the number Nx of things xi (i=1,..,Nx) constituting the present universe. Reasoning for the further extension to “All” is provided in the derivation of the "Fundamental Equation"
In a second step a value is attributed to each thing.
The universe W existing according to above mereological axiom has part all things and accordingly must be greater or equal than the sum of the values of things:
\[W \geq\sum_{i=1}^{N_x}x_i\]
Adding a further thing x0 - named the vacuum or the matrix thing - generates equality:
\[W = x_0 +\sum_{i=1}^{N_x}x_i\]
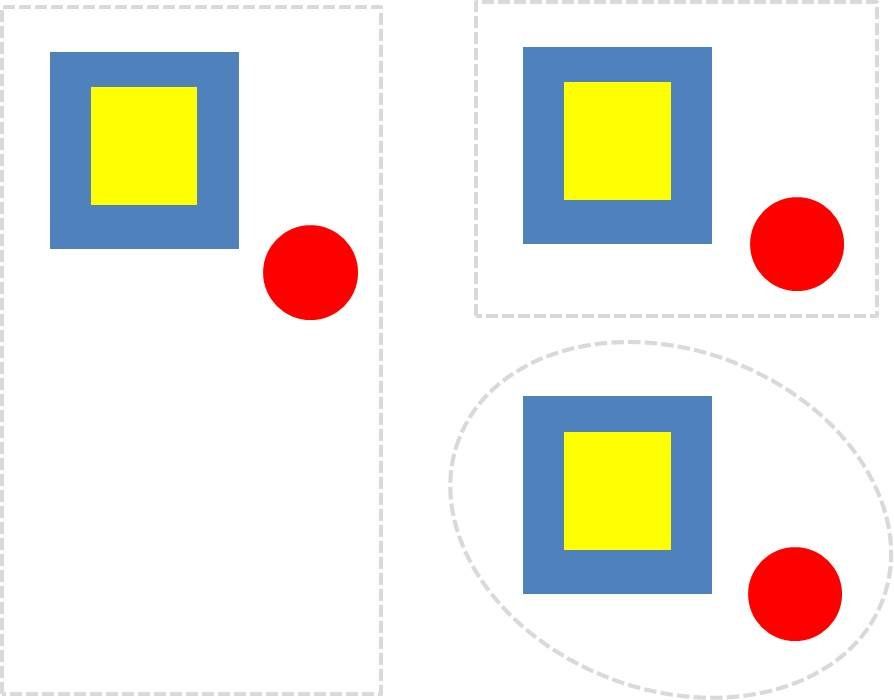
Figure: Different “matrix” things x_0 (marked by gray dashed boundaries) enclosing the same set of things (blue, yellow, red). They all have_part all other things and thus represent possible universes according to the mereology axiom.
The relative size and shape of the x_0 domains may differ.
Selecting one of the x_0 fixes the universe U under consideration:
\[U =\sum_{i=0}^{N_x}x_i\]
The universe U according to this expression is the sum of its parts including the matrix. In a further quantification step one can “normalize” this universe getting the numerically quantified value “1”:
\[1=\sum_{i=0}^{N_x} \frac {x_i} U\]
Renaming the xi/U - being the fractions of the universe - to i eventually leads to the “basic equation”:
\[1=\sum_{i=0}^{N_\Phi} \Phi_i\]
(Basic Equation)This "basic equation" - expressed in words - reads:
Several assumptions have been made above to motivate this formula on the basis of a mere logical expression. While a strong need for a rigorous derivation arises, quite a number of important conclusions can be drawn from further investigating this formula in detail. On this website all “things” are interpreted as being fractions of the universe with their individual values all ranging from 0 to 1:
The “whole” is the sum of its fractions
(including the matrix as a fraction)
(including the matrix as a fraction)
Several assumptions have been made above to motivate this formula on the basis of a mere logical expression. While a strong need for a rigorous derivation arises, quite a number of important conclusions can be drawn from further investigating this formula in detail. On this website all “things” are interpreted as being fractions of the universe with their individual values all ranging from 0 to 1:
\[0\leq \Phi_i \leq1 \]
If a thing is “existent” it takes a non-zero value:
\[0 < \Phi_i \leq1 \]
If a thing is “non-existent” (or “not yet existent” or “no more existent”) it takes exactly the value zero with the potential of changing to a non-zero value i.e. with the potential of becoming an existent thing:
\[0=\Phi_i \]
If a thing is the only existent it takes exactly the value 1:
\[1=\Phi_i \]